menghitung konvolusi sirkular


Perhitungan Konvolusi Sirkular
Untuk mengetahui bagaimana metoda untuk menghitung konvolusi sirkular, perhatikan contoh berikut:
Diketahui urutan yang pertama: x = {1, 2, 3, 4, 5, 6} dan uruta yang kedua: h = {7, 8, 9, 3}. Tentukan ! 

Jawab:
Langkah 1:
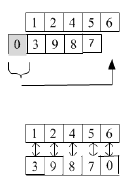
Gambarkan kedua urutan tersebut secara bertumpuk, urutan pertama di atas urutan kedua, dan tambahkan padding berupa angka 0 agar ukuran urutan kedua sama dengan urutan pertama:

Langkah 2:
Putar urutan h, sehingga komponen pertama menjadi kelima, kedua menjadi keempat, dan seterusnya. Sebut urutan ini menjadi h’:
Langkah 3:
Geser urutan h’ ke kiri sehingga komponen kelima dari h’ berada di bawah komponen pertama dari x:


Posisi ini adalah posisi awal yang paling penting!!
Langkah 4:
Untuk mencari y[0], posisi awal ke kanan sejauh 0 satuan. Dalam hal ini berarti tidak ada pergeseran:

Langkah 5:
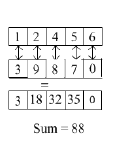
Pindahkan komponen pertama, kedua, ketiga, dan keempat dari h’ ke sebelah kanan:

Langkah 6:
Lakukan perkalian antara komponen yang bertumpuk, dan jumlahkan hasilnya:


Hingga langkah ini telah didapat bahwa y[0] = 112.

Langkah 7:

Geser semuanya kembali ke posisi awal, kemudian untuk mencari y[1], geser posisi awal ke kanan sebanyak 1 satuan:

Langkah 8:
Lakukan seperti langkah 5, namun kali ini pindahkan komponen pertama, kedua, dan ketiga dari h’ ke sebelah kanan:

Langkah 9:
Lakukan seperti langkah 6, lakukan perkalian antara komponen yang bertumpuk, dan jumlahkan hasilnya:


Pada langkah di atas dapat dilihat bahwa komponen yang bernilai 1 (pada saat x[0]) bertumpuk dengan komponen yang bernilai 8 (pada saat h[0]), oleh karena itu, nilai di atas adalah untuk y[0], sedangkan nilai sebelumnya adalah untuk y[-1].
Jadi hingga langkah ini didapat y[-1] = 112 & y[0] = 91.
Langkah 10:
Lakukan seperti langkah 7, geser semuanya kembali ke posisi awal, kemudian untuk mencari nilai y yang selanjutnya, geser posisi awal ke kanan sebanyak 2 satuan:



Langkah 11:
Pindahkan komponen pertama dan kedua dari h’ ke sebelah kanan:



Langkah 12:
Kalikan komponen yang bertumpuk dan jumlahkan hasilnya:

Nilai di atas adalah untuk y[1].
Langkah 13:
Lakukan seperti langkah 7, geser semuanya kembali ke posisi awal, kemudian untuk mencari nilai y yang selanjutnya, geser posisi awal ke kanan sebanyak 3 satuan:


Langkah 14:
Pindahkan komponen pertama dari h’ ke sebelah kanan:


Langkah 15:
Kalikan komponen yang bertumpuk dan jumlahkan hasilnya:


Hasil di atas adalah untuk y[2]
Langkah 16:
Kembalikan ke posisi awal, untuk mencari nilai y selanjutnya geser h’ ke kanan sebanyak 4 satuan:



Langkah 17:
Tidak ada komponen yang perlu dipindah, langsung saja kalikan komponen yang bertumpuk dan jumlahkan semuanya:


Hasil di atas adalah untuk y[3].
Seluruh tahapan selesai apabila walaupun tidak digeser-geser, seluruh posisi komponen h’ telah tepat bertumpuk di bawah x. Sehingga nilai akhirnya adalah:
y = {112, 91, 71, 88, 124}

Telah diketahui bahwa hasil konvolusi dari dua buah urutan bersesuaian dengan hasil perkalian antara Transformasi Fourier kedua urutan tersebut:


Jika didefiniskan Transformasi Fourier berikut:


Maka:

Dari pengertian konvolusi sirkular w[n]:

Maka:

Jika x[n] dan h[n] adalah urutan dengan panjang N, maka w[n] juga akan memiliki panjang N. Namun, y[n] memiliki panjang maksimum (2N - 1).
Contoh:
Diketahui dua sinyal diskrit:


Tentukan konvolusi sirkuler dari x1(n) dan x2(n) menggunakan definisi dan perkalian dua DFT
Jawab :


















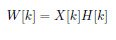
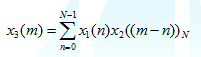
Komentar

Posting Komentar

Postingan populer dari blog ini

Mengatur RPM Motor Encoder/Rotary Encoder dan Sensor Suhu LM35 Berbasis Arduino

Gambar
"Motor Encoder/Rotary Encoder dan Sensor Suhu LM35" Assalamualaikum Wr Wr. Pada artikel kali ini, saya akan berbagi ilmu sederhana mengenai bagaimana mengatur Rpm Motor Encoder/Rotary Encoder dan Sensor Suhu pada Aplikasi Proteus berbasis arduino. 1. Motor Encoder/Rotary Encoder Secara umum prinsip kerja rotary encoder ini dapat diilustrasikan sebagai berikut. Dua buah sensor optis (Channel A dan B) pendeteksi “hitam dan putih” digunakan acuan untuk menentukan arah gerakan. Searah jarum jam (clock-wise, CW) atau (counter clock-wise, CCW). Sedangkan jumlah pulsa (baik A atau B) dapat dihitung (menggunakan prinsip counter) sebagai banyak langkah yang ditempuh. Dengan demikian arah gerakan dan posisi dapat dideteksi. Contoh rotary encoder. Biasanya encoder ini dipasang segaris dengan poros (shaft) motor, gearbox, sendi datau bagian berputar lainnya. Beberapa tipe encoder memiliki poros berlubang (hollow shaft encoder) yang didesain untuk ...
Baca selengkapnya

Cara Kerja Backpropagation

Gambar
Arsitektur : Dalam metode Backpropagation, biasanya digunakan jaringan multilayer. Pada gambar, unit input dilambangkan dengan X, hidden unit dilambangkan dengan Z, dan unit output dilambangkan dengan Y. Bobot antara X dan Z dilambangkan dengan v sedangkan bobot antara Z dan Y dilambangkan dengan w. Seperti yang diperlihatkan pada gambar diatas bahwa jaringan Backpropagation terdiri dari 3 sel neuron pada lapisan input yaitu x1,x2,dan x3; 2 sel neuron pada lapisan tersembunyi yaitu z1 dan z2; serta 1 sel neuron pada lapisan output yaitu y. Nilai bias  b1 yang di berikan pada lapisan tersembunyi bertujuan untuk mengolah data input ditambah bobot Vij yang masuk ke dalam sel-sel pada lapisan tersembunyi dengan bantuan fungsi aktifasi. Begitupula dengan nilai bias b2 yang diberikan pada lapisan keluaran adalah untuk mengolah data yang berasal dari keluaran sel pada lapisan tersembunyi ditambah bobot Wij yang masuk kedalam lapisan keluaran dengan bantuan fungsi aktifasi. Cara Kerja :...
Baca selengkapnya