analisa rangkaian sekuensial

14.1 Analisa Rangkaian Sekuensial

Untuk menganalisis rangkaian sekuensial diperlukan:

•     State  table  (tabel state) menunjukkan input, output, dan perubahan  state pada rangkaian sekuensial.

•     State diagram (diagram state) merupakan alternatif cara untuk menunjukkan informasi yang sama.

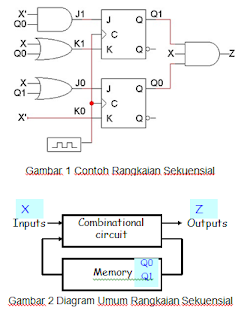
Gambar 1 berikut ini adalah rangkaian sekuensial dengan 2 buah JK flip-flop. Pada rangkaian ini terdapat 1 buah input, X dan 1 buah output, Z. Nilai flip-flop (Q1Q0) adalah dari state, atau memori rangkaian. Output flip-flop pun kembali ke gerbang sebelah  kiri.  Hal  ini  sesuai  dengan  diagram  umum  rangkaian  sekuensial  pada gambar 2.

Untuk menganalisis rangkaian kombinasional digunakan tabel kebenaran. Sebuah state table merupakan analogi sekuensial dari tabel kebenaran. Dimana memperlihatkan input dan state saat itu (current state) di sebelah kiri tabel dan output dan state selanjutnya (next state) di sebelah kanan. Untuk rangkaian sekuensial,  outputnya  tergantung  dari  input dan  juga  current  state  dari  flip-flop. Dalam rangka penentuan output, kita pun perlu menentukan keadaan/state flip -flop pada siklus clock selanjutnya. Tabel state dasar untuk rangkaian pada gambar 1 di atas ditunjukkan pada tabel 1 berikut. Ingat bahwa hanya ada 1 input yaitu X dan 1 output  Z,  dan  2  buah  flip-flop  Q1Q0.  Present  state  Q1Q0  dan     input  akan menentukan next state dan output rangkaian.

14.1. 1 Menentukan Output

Hal  yang  paling  mudah  untuk  dilakukan  adalah  menentukan  output.  Output rangkaian sekuensial pada contoh ini tergantung dari current state – Q0 dan  Q1 – dan input. Dari diagram pada gambar 1, kita dapat melihat bahwa output pada waktu

tertentu (current time) :

Z = Q1Q0X………………………………………….(1)

Dengan demikian tabel statenya menjadi seperti tabel 2 berikut.

14.1.2 Menentukan State Selanjutnya (Next State)

Menentukan next state lebih sulit dibandingkan menentukan output. Untuk mendapatkannya kita harus mengetahui bagaimana flip-flop berubah. Terdapat beberapa langkah proses yang harus dilakukan.

Langkah 1: Tentukan persamaan Boolean dari input flip-flop, yaitu bagaimana input

(mis: J & K) untuk flip-flop tergantung pada current  state dan input . Langkah 2: Gunakan persamaan ini untuk menentukan nilai aktual dari input flip-flop

untuk setiap kombinasi yang memungkinkan dari present state dan input,

yaitu mengisi tabel state (dengan kolom tengah baru).

Langkah 3: Gunakan tabel karakteristik atau persamaan flip-flop untuk menentukan

Next state, berdasarkan pada nilai input flip-flop dan present state.

14.1.2.1 Langkah 1: Menentukan Persamaan Input Flip-flop

Dari gambar 1 di atas dapat ditentukan persamaan input flip-flop adalah:

J1 = X’ Q0……………………………………………(2) 

K1 = X + Q0……………………………………….….(3)

 J0 = X + Q1…………………………………………..(4) 

K0 = X’………………………………………………..(5)

Tiap JK flip-flop mempunyai 2 buah input, J dan K. (D dan T flip-flop memiliki 1 input).

14.1.2.2 Langkah 2: Menentukan Nilai Input Flip-flop

Dengan persamaan 2 s/d 5 di atas, kita dapat membuat tabel yang menunjukkan nilai J1, K1, J0 dan K0  untuk kombinasi yang berbeda dari present state Q1Q0 dan input X (dapat dilhat pada tabel 3).

14.1.2.3 Langkah 3 : Menentukan State Selanjutnya (Next State)

Terakhir, gunakan tabel atau persamaan karakteristik JK flip-flop untuk menentukan state selanjutnya (next state) untuk setiap flip-flop, berdasarkan pada present state dan input.

Persamaan karakteristik umum JK flip-flop adalah:

Q(t+1) = K’Q(t) + JQ’(t)…………………………………..(6)

Dalam rangkaian contoh, kita menggunakan 2 JK flip-flop, sehingga kita harus mengaplikasikan persamaan ini untuk keduanya:

Q1(t+1) = K1’Q1(t) + J1Q1’(t)……………….…………..(7)

Q0(t+1) = K0’Q0(t) + J0Q0’(t)………………..………….(8)

Selain dengan cara di  atas kita pun dapat menentukan  next state  untuk setiap kombinasi input/current state secara langsung dari tabel karakteristik.     Tabel karakteristik JK fli-flop ditunjukkan pada tabel 4 di bawah ini.

14.1.3 Mendapatkan Langsung Kolom pada Tabel State

Tabel dimulai dengan Present State dan Input.

•     Present State dan Input akan menghasilkan input flip-flop (FF Input).

•     Present State dan FF Input menghasilkan Next State, berdasarkan pada tabel karakteristik flip-flop.

•     Present State dan Input menghasilkan Output.

Kita hanya mempedulikan FF Input untuk memperoleh Next State.

Catatan: Output terjadi pada siklus saat ini dan Next State pada siklus selanjutnya. Dengan demikian akan diperoleh tabel state lengkap untuk rangkaian contoh di atas seperti yang ditunjukkan pada tabel 6.

14.1. 4 Membuat Diagram State

Kita  dapat  merepresentasikan  tabel  state  dalam  bentuk  grafik  dengan  sebuah diagram state. Diagram ini tergantung pada tabel state rangkaian  contoh di atas (tabel 7). Dengan demikian akan dihasilkan diagram state seperti pada gambar 3 berikut.

Periksa selalu ukuran dari diagram state .

•     Jika terdapat n flip-flop, akan ada 2n node dalam diagram.

•     Jika terdapat m input, maka tiap node akan memiliki  2m panah keluar dari setiap state.

Dalam contoh ini, rangkaian memiliki 2 buah flip-flop dengan demikian memiliki 4 buah state atau node. Rangkaian in hanya memiliki 1 buah input, sehingga setiap node memiliki 2 panah keluar.

14.2 Sintesa Rangkaian Sekuensial

Proses sintesa kebalikan dari proses analisa:

•     Pertama kita buat tabel dan diagram state untuk menunjukkan komputasi.

•     Kemudian kita buat rangkaian sekuensialnya.

Berikut ini merupakan prosedur sintesa rangkaian sekuensial :

Langkah 1:

Buat tabel state berdasarkan pernyataan masalah (problem statement). Tabel harus memperlihatkan present state, input, next state dan output. Dapat juga lebih mudah dibuat diagram state terlebih dahulu kemudian dikonversikan dalam bentuk tabel. Langkah 2:

Menetapkan kode biner untuk state pada tabel state. Jika terdapat n state, kode biner memiliki sekurangnya log2 n digit, dan rangkaiannya akan memiliki sekurangnya log2 n flip-flop.

Langkah 3:

Untuk setiap flip-flop dan setiap baris pada tabel state, tentukan nilai input flip-flop yang diperlukan untuk menghasilkan next state dari present state. Disini kita dapat menggunakan tabel eksitasi flip-flop.

Langkah 4:

Tentukan persamaan sederhana dari input dan output flip-flop.

Langkah 5:

Buat rangkaiannya!

Sebagai contoh, kita akan merancang rangkaian Sequence Recognizer. Sequence recognizer adalah jenis rangkaian sekuensial yang mencari pola bit khusus pada inputnya.

Rangkaian ini hanya memiliki satu input, X.

•     Satu bit input disediakan pada setiap siklus clock. Sebagai contoh, diperlukan

20 siklus untuk membaca input 20-bit.

•     Merupakan  cara  yang  mudah  untuk  memasukan  input  sekuensial  yang panjang.

Terdapat 1 buah output, Z, dimana akan bernilai 1 jika didapatkan pola yang diinginkan.  Contoh: rangkaian mendeteksi pola bit “1001”:

Input:   11100110100100110 …

Output: 00000100000100100 …

Disini, satu bit input dan output muncul tiap siklus clock. Dengan demikian memerlukan rangkaian sekuensial karena rangkaian harus mengigat input dari siklus clock sebelumnya, untuk mengetahui apakah ada pola bit yang cocok atau tidak.

14.2.1 Langkah 1: Membuat Tabel State

Hal terpenting yang harus dipahami adalah bagaimana state digunakan secara tepat untuk memecahkan masalah yang diberikan.

•     Buat    tabel    state    berdasarkan    pernyataan    masalah.    Tabel    harus memperlihatkan present state, input, next state dan output.

•     Terkadang  lebih  mudah  untuk  membuat  diagram  state  terlebih  dahulu kemudian dikonversikan dalam bentuk tabel.

Ini merupakan langkah yang paling sulit. Setelah kita dapatkan tabel state, prosedur perancangan selanjutnya adalah sama untuk semua rangkaian sekuensial.

14.2.1.1 Menentukan State dan Diagram State Dasar

State apa yang dibutuhkan untuk sequence recognizer?

•     Input dari siklus clock sebelumnya harus diingat.

•     Contoh: jika input sebelumnya adalah 100 dan input saat ini (current input)

adalah 1, maka outputnya harus bernilai 1.

•     Secara  umum,  kita  harus  mengingat  kemunculan  dari  bagian  pola  yang diinginkan- dalam kasus ini, 1, 10, dan 100.

Dimulai dengan diagram state dasar (label input/output) pada gambar 4 dengan keterangan state pada tabel 8.

14.2.1.2 Mendeteksi Kemunculan Overlapping

Apa yang terjadi jika kita ada dalam state D (input ketiga terakhir 100), dan nilai current  input  adalah  1?  Outputnya harus 1,  karena  kita  menemukan  pola  yang diinginkan. Namun demikian, nilai 1 terakhir ini harus dapat menjadi nilai awal bagi kemunculan pola selanjutnya. Sebagai contoh, 1001001 berisi 2 kemunculan 1001. Untuk mendeteksi kemunculan pola yang overlapping, nilai next state harus B. Perhatikan panah pada diagram state (gambar 5) berikut.

14.2.1.3 Melengkapi Diagram State

Hal selanjutnya adalah melengkapi diagram state dengan mengisi panah yang lain. Ingat bahwa diperlukan 2 buah panah keluar untuk setiap node, untuk mengatasi

kemungkinan dari X=0 dan X=1. Dengan demikian akan didapatkan diagram state

pada gambar 6 di bawah ini.

14.2.1.4 Membuat Tabel State dari Diagram State

Terakhir buat tabel state dari diagram state di atas. Ingat bagaimana hubungan panah diagram state dengan baris pada tabel state. Perhatikan gambar 7 berikut. Dengan demikian akan dihasilkan tabel state seperti yang ditunjukkan pada tabel 9 di

bawah ini.

14.2.2 Langkah 2: Menetapkan Kode Biner untuk State

Kita memiliki 4 state ABCD, dengan demikian kita memerlukan sekurangnya 2 buah flip-flop Q1Q0. Hal yang mudah untuk dilakukan adalah merepresentasikan state A dengan Q1Q0 = 00, B dengan 01, C dengan 10, dan D dengan 11. Penetapan state ini mempengaruhi kompleksitas dari rangkaian. Isi kolom present state pada tabel di

atas diganti dengan nilai kode biner untuk state A, B, C dan D. Sehingga  akan diperoleh tabel state sebagai berikut (tabel 10).

14.2.3 Langkah 3: Menentukan Nilai Input Flip-flop

Selanjutnya,  kita  harus  mengetahui  bagaimana  membuat  flip-flop  berubah  dari present state ke dalam next state yang diinginkan. Hal ini tergantung dari jenis flip- flop yang kita gunakan. Jika kita gunakan JK Flip-flop. Setiap flip-flip Qi, lihat nilai present dan  next  state,  dan  tentukan  berapa seharusnya  input  Ji dan  Ki  untuk membuat state berubah.

Lihat kembali karakteristik tabel JK  (tabel 4).  Jika present state dari JK flip-flop adalah 0 dan kita menginginkan nilai next state menjadi 1, maka terdapat 2 pilihan untuk input JK:

•     Kita dapat menggunakan JK=10, untuk secara eksplisit membuat set flip-flop next state menjadi 1.

•     Kita pun dapat menggunakan  JK=11, untuk melakukan complement pada current state 0.

Jadi untuk mengubah dari 0 menjadi 1, kita harus men-set J=1, tetapi K dapat bernilai 0 atau 1. Dengan cara yang sama, transisi state yang mungkin lainnya dapat dilakukan dalam dua cara yang berbeda.

Tabel eksitasi (excitation table) menunjukan berapa nilai input flip-flop input yang diperlukan untuk  membuat perubahan  state  yang  diinginkan. Informasinya  sama seperti yang diberikan dalam tabel karakteristik tetapi dipresentasikan dalam arah kebalikan. Tabel eksitasi JK flip-flop ditunjukkan pada tabel 11.

Kita dapat menggunakan tabel eksitasi JK di atas untuk mencari nilai yang benar untuk setiap input flip-flop, berdasarkan present dan next state. Semua nilai input JK flip-flop dimasukkan pada kolom tabel 12 berikut.

14.2.4 Langkah 4: Menentukan Persamaan Input dan Output Flip-flop Selanjutnya, kita dapat membuat K-map dan menentukan persamaan untuk keempat input flip-flop, dan juga output Z. Persamaan ini adalah dalam kondisi present state dan input. Keuntungan dari menggunakan JK flip-flop adalah terdapat banyak kondisi yang  diabaikan  (don’t  care),  dengan  demikian  persamaannya  lebih  sederhana.

Sehingga akan didapatkan :

J1 = X’ Q0……………….…………………………….(9)

K1 = X + Q0………………….………………………(10) 

J0 = X + Q1………………….……………………….(11) 

K0 = X’……………………….………………………..(12)

 Z = Q1Q0X…………………………………………..(13)

14.2.5 Langkah 5: Buat Rangkaian

Terakhir,  kita  gunakan  persamaan  yang  sederhana  tersebut  untuk  membangun rangkaian lengkap (gambar 8).

14.2.6 Diagram Pewaktuan (Timing Diagram)

Gambar 9 berikut ini adalah contoh diagram pewaktuan dari sequence recognizer.

•     Flip-flop Q1Q0 mulai pada kondisi awal, 00.

•     Pada  tiga  tepi  clock  positif  pertama,    X  bernilai  1,  0,  dan  0.  Input  ini menyebabkan Q1Q0 untuk berubah, sehingga setelah tepi ketiga nilai Q1Q0

= 11.

•     Kemudian ketika X=1, Z menjadi 1, berarti ditemukan 1001.

Output Z tidak perlu berubah pada tepi positif clock, melainkan dapat berubah ketika

X berubah karena Z = Q1Q0X.

14.2.7 Membuat Rangkaian dengan D Flip-flop

Bagaimana jika kita menggunakan D flip-flop untuk membangun rangkaian sequence recognizer/detector ? Kita telah mendapatkan tabel state dan menentukan kode biner untuk state. Dengan demikian kita mulai dari langkah 3, menentukan nilai input flip- flop. D flip-flop hanya memiliki satu input, sehingga hanya diperlukan 2 kolom pada tabel untuk D1 dan D0.

Tabel eksitasi D Flip-flop ditunjukkan pada tabel 13 di bawah ini. Dari tabel eksitasi ini akan dihasilkan tabel 14 sebagai berikut.

Langkah selanjutnya (langkah 4) adalah menentukan persamaan input D flip-flop.

Dari K-Map didapatkan:

D1 = Q1 Q0’ X’ + Q1’ Q0 X’…………………………..(14) D0 = X + Q1 Q0’……………………………………….(15) Z = Q1 Q0 X……………………………………………(16)

Selanjutnya adalah membuat rangkaian berdasarkan persamaan input dan output diatas  (langkah 5).  Diagram  rangkaian  Sequence  Recognizer  dengan  D flip-flop ditunjukkan pada gambar 10.

14.2.8 Perbandingan Realisasi Flip-flop

JK flip-flop baik digunakan karena terdapat banyak nilai yan diabaikan (don’t care)

dalam input flip-flop, yang membuat rangkaian akan menjadi lebih sederhana.

D flip-flop memiliki keuntungan yaitu kita tidak perlu men-set input flip-flop sama sekali karena nilai Q(t+1) = D. Meskipun demikain, persamaan input D biasanya lebih kompleks dibandingkan dengan persamaan input JK.

Pada parakteknya, D flip-flop lebih sering digunakan.

–     Hanya terdapat 1 buah input untuk setiap flip-flop.

–     Tidak ada tabel eksitasi yang perlu dikhawatirkan.

–     D  flip-flop  dapat  diimplementasikan  dengan  perangkat  keras  yang  lebih sedikit dibandingkan dengan JK flip-flop.